2023情報I 2学期
第5回 授業の振り返りより
質問より
- 引き算を足し算にするときなぜ-6を+4とするのかが気になった。/足し算の+8+8+8...が足し算にするためなのはわかったけど、どこから8が出てきたのかがわからなかった。/-6を4に置き換える手間も必要ってこと?10+(-6)をしているの?
- 教科書の説明は気にしないよう授業で説明しました。10進法なので理解しても意味がありません。「引き算は足し算に置き換えられる」「割り算は引き算の繰り返し」ということだけ理解してください。授業で説明したとおり、2進法の負の数を使えば引き算を足し算にできますよね。引き算が足し算でできるようになったので、割り算も足し算でできるわけです。
- 二進法の正の数を負の数にするときに、どうして反転して1を足す、という方法がうまくいくのか不思議に思った。/なぜ二進法の負の数は反転させて1を足すと求められるのですか。
- 元の数と反転した数を足してみてください。すべての桁が1になります。この数に1を足すと、繰り上がって1桁増え、元からある桁はすべて0になります。増えた1桁は捨てるんでしたよね。つまり0になります。元の数+反転した数+1=0ということです。
5に加えると0になる数を-5と定義しました。元の数に反転した数+1を加えると0になるのですから、反転した数+1は負の数になるということです。
- NOT回路にだけ小さい丸があるのはなぜだろう?
- ○は否定、値の反転を意味します。△だけなら変化なし、○がついているのでNOTになるんです。
- 多い桁数の2進法の計算も加算機を重ねることでできるようになるのですか。
- そうなりますよね。
- 半加算器と全加算器の関係、どのようなものかがわかりませんでした。
- 半加算器は1桁+1桁を計算すると、答えと繰り上がりの2桁になります。2つの数を入力して、2つの数が出力されます。2桁+2桁の計算をするには、繰り上がりを含めて3つの入力を処理する必要があります。そのために利用するのが全加算機です。
- それぞれのプログラミング言語の裏には加算器がいくつもあるということですか。
- プログラミング言語はソフトウェアの話です。加算機はCPU内部の物理的な回路です。まったく別の話ですね。
- あらかじめ、ビット数を決めるとあったが、何ビットが基本的なのか
- 32bitや64bitが一般的です。
- なぜサイトによって、計算の値が少し違ったのか
- サイトではなくExcelとPythonというプログラムの計算結果が違うということですよね。内部的な数値の表現や計算の仕方、表示の仕方が違うからだと考えられます。
- スーパーコンピューターの富岳はどのくらいのビット数で計算してるのか気になりました。また、現時点では何ビットがげんかいなのでしょうか?
- 富岳は64ビットコンピュータだそうです。ビット数を増やすには、内部のCPU全体の構造や構成を新たに設計し、それを活用するプログラムを全部作る必要があります。限界はないので処理ビット数を増やすことは可能だと思いますが、莫大な費用がかかり、汎用性のないものができあがります。
- 教科書の隅に書いてある昔はビット数が足りないからバグが起きたということは、今あるバグが多いゲームはビット数が少ないということですか?また、海外のゲーム(マイクラなど)は日本のゲーム(ゼルダの伝説など)よりバグが起きやすい印象があるのですが、それはビット数が少ないからという理由なのでしょうか?
- 違います。昔のコンピュータ(ゲーム機)はごく限られた記憶容量等を活用していたためです。バグが多いプログラムはテストが十分におこなわれていないだけです。
- 三桁同士の計算は筆算でできますか?
- 10進法の3桁同士の計算、できますか?できますよね。同じ方法で筆算すればできますよ。
- 論理回路はコンピューター内でどのような場面で利用されているのですか。
- CPUの中は論理回路で構成されています。コンピュータのすべての計算は論理回路でおこなわれています。
- Pythonなどで計算したとき、合っているものと期待していた答えと異なってしまうのはなぜか教えてください。
- 計算するときに事前にどのくらい精度が必要か指示していないからです。
- phythonやExelで計算の性能が変わるのはなぜですか?
- PythonもExcelも計算のさせ方が違うからです。同じ計算をしても、機械語レベルで同じ命令をしているとは限りません。
- ExcelやPythonで計算した時、0.1が上手く表示されなかったのですが、なぜ0.1にコンピューターは弱いのですか?
- 10進法の0.1を2進法で表現すると、0.00011001100・・・と循環小数になってしまいます。どこかの桁で記録を打ち切ると、誤差が出ますよね。
- 4.3-4.2などの現在AIが苦手とする数字は将来的には解けるようになりますか?また、どうやったら解けるようになるのですか?
- 何ビットで数を表現するかによって誤差が決まります。解決できていないわけではありません。もっと正確にするには、ビット数を増やせばいいわけです。現状、あんな小さな誤差で困ります?困る場合はビット数を増やして計算してください。
- 聞き逃してしまったので教えてほしいです。3つで全加算器になるのですか。
- 全加算機は半加算機2つとORを組み合わせて作ります。教科書にある回路図の通りです。
- NAND回路やNOR回路、XOR回路は何のためにあるんですか?またいつ使うんですか?
- 基本論理回路にはいろいろあって、適材適所で使い分けます。AND・OR・NOT以外の論理回路を使って半加算機や全加算機を作ることができます。
- 10進法を10進法のまま扱えるコンピューターはあるのか?
- ないです。何度も説明していますが、10段階を正確・高速に表現することができないため、はっきりした2段階の2進法を使います。
- 論理回路は、機器の中に物体(目に見えるもの)として存在するんですか。
- 物体として存在しますが、見るには電子顕微鏡が必須で、電子顕微鏡でも難しいかもしれません。
- 0.3-0.2は正確に計算できたのに、なぜ0.3と0.2にそれぞれ4を足しただけの4.3-4.2で誤差が生じるのだろうか。
- わかりません。可能なら研究してみてください。
- 論理回路シミュレータSimcirJSにある全加速器の左上に書いてある「Cin」と右下に書いてある「Cout」にはどのような意味があるのか
- Cは繰り上がり(Carry)の略語です。繰り上がりの入力がCin、出力がCoutですね。
- コンピュータが足し算を使わずに掛け算や割り算を行うことはできるようになりますか。
- できますよ。できますけど、足し算やっている間、掛け算回路や割り算回路が無駄になりますけど。
感想より
- excelは0.3-0.2=0.1と計算できるのに、同じ差の4.3-4.2だと0.0999…となるのが不思議だった。コンピューターはこのような簡単な計算が苦手だと分かって、もしかしたら人間のほうがコンピューターより賢いのかも、と思った。
- 人間は10進法のルールに基づき計算しますが、コンピュータは2進法に直して計算するので、どうしても表現ができない数が出てきます。10進法の小数で1÷3の答え、正確に言ってください。できませんよね。それと同じことなんです。
- 二進法であらわせない数があるように、十進法にも表せない数があるのだろうか
- たとえば、3進法を使うとすると、10進法の1/3は3進法で0.1となります。10進法だと正確に表現できませんよね。2進法の小数で表された数は、必ず10進法の小数で表現できます。なぜなら、10は2で割り切れるからです。
- Pythonでの計算結果が正確でなかったことに驚いた。同時にExcelのほうが計算結果がより正確に出るということにも驚いた。計算するのに使うアプリの違いによって、どの数字の計算が得意・不得意なのかわかれることを初めて知り、何でもかんでも特定のアプリを使うのではなく、それぞれのアプリの特徴をよく知ったうえで場合に応じてうまく活用することが大切なんだなと感じた。
- 2正確でないということではなく、どこの桁までの精度を確保するかによって10進法による表示が変わってしまうということです。1÷3の答えを小数で正確に答えること、できますか?ある程度の桁で終わりにすると、その部分で誤差が発生するのです。
- コンピュータのビット数が限られていて、それに収まる計算や処理しかできないことは、最近よく耳にするようになってきた2038年問題に関わってくる内容で、興味深かった。また論理回路は、マインクラフトのレッドストーン回路というもので再現することができるので、遊び感覚でやってみたいと思った。
- 2 2038年問題は、コンピュータの日付・時刻が1970年1月1日0時0分0秒スタートだった場合、2038年1月19日12時14分7秒で32bitを超え、正しく表せなくなってしまう(あふれてしまう)ことですね。桁あふれの典型的な例です。
- コンピュータでの計算結果は本来のものとすこし違う値をだすが、これはコンピュータが間違えているのではなく、扱える範囲や値の精度に限りがあるためであると知った。
- ゲームのオーバーフローと呼ばれる現象もこのようなコンピューターの演算ミスから生まれてるのだなと分かった。時に、とある昔のシュミレーションゲームで平和主義の値を下げるとオーバーフローを起こし、あのガンディーが核兵器をバンバン使う独裁者に豹変することがあったそうです。この仕組みは現在の仕組みのゲームで起こってもとても面白いんじゃないかと思ったので、オーバーフロー自体の仕組みについて『この中身はどうなっているのか』と気になって少し調べてみることにします。
- 順序を追って一つずつというのがコンピュータの特徴なのだと思った
- いつもより予習を意識してしっかりやったつもりでした。内容が簡単だったのかもしれませんが、いつもより理解が少し深く、自分のわからない事や考えが浮かんだおかげで質問ができた。これからもできる限り精度をキープしたい。
- and or notの回路がわかった。出力するものが1になると豆電球がつくのが面白かった。負の数を二進法で表してそれを足し算するのは、はみ出た5ビット目を消せば表の通りになるのかすごくすっきりした。
- 2進法で計算することのすごさが分かった。負の数を時計で例えると分かりやすかった。
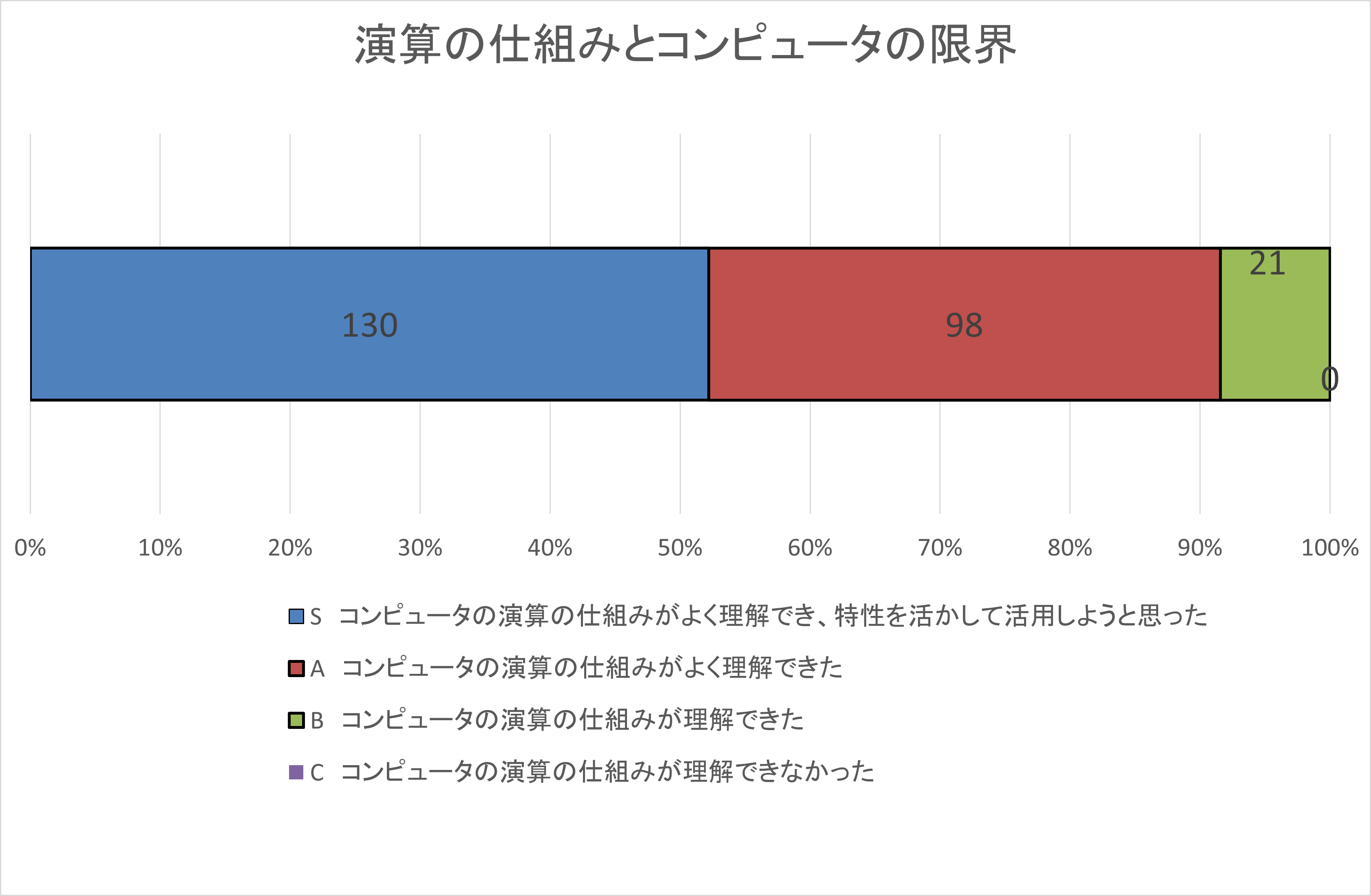
自己評価集計
ワードクラウド
- 3つのキーワード

- 感想や気づき

テキストマイニング 無料ツール by ユーザーローカル
前のページに戻る



