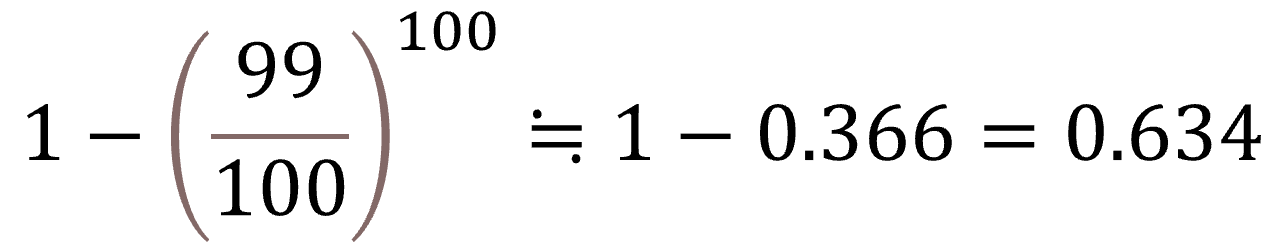2022情報I　2学期
第20回　授業の振り返りより

質問より

排出回数が多くても当選人数がそこそこなのは、同じ人に何度も当たっているということ、という解釈で合っていますか。

画面に表示されるシミュレーション結果について、理解できていないようですね。Excelでシミュレーションしても、Pythonでシミュレーションしても、あたりの回数を表示するようになっています。全部外れた人（0回の人)もいれば、3回当たっている人もいたはずです。表示される結果を確認し、プログラムや計算式を理解しながら進めれば理解できるはずです。

サイコロを１０００回振ると１の目ばかり出てしまうのはなぜですか？

Excelでシミュレーションしましたね。サイコロの目をカウントする式を1の目だけ修正して、2～6の目はコピーするよう、説明のスライドには書いてありました。状況からすると、このコピーを忘れたのだと思います。1～6の目が出た数の合計を見ると、1000になっていないはずです。1000回シミュレーションしたはずなのですから、「おかしいな」と気づけるようになってくださいね。

先生の画面のタスクバーに出ている黄色いにこちゃんは何ですか。

WingnetというPC教室管理用のソフトウェアです。Wingnetの機能を使って皆さんの画面をモニターしたり、チャットしたり、ファイルをデスクトップに配ったりしています。

疑似乱数はどのように生成されているのですか。

疑似乱数を生成する仕組みは、ここで説明できるほど簡単ではありません。以下のページを読んでみてください。
乱数の仕組み

前回、生命体の増加のシミュレーションをＥｘｃｅｌでやったのですが、途中までしか終わらなかったので名前を変えることを知らずにそのままの名前で保存してしまいました。直した方がいいですか。

ファイル名を指定するのは、提出を求めているときと、同一のファイル名で誤って上書き保存をすることを防ぐ配慮をしているときです。今回は提出を求めていませんから、そのままの名前で保存して問題なければそのままでかまいません。

ガチャの確率的シミュレーションをExcelで行ったのですが、シミュレーション結果を再計算しても結果が消えないように残して１００回ほど繰り返し、集計してグラフ化したかったのですが、うまくできませんでした。地道にコピーして、値としてペーストしてみたのですが、当然時間がかかります。何か良い方法はないでしょうか？

100人の100連ガチャのExcelシートを100回分データ保持して分析するということですか？同じことの繰り返しなので、プログラムを書くとよいでしょう。ExcelにはVBA（Visual Basic for Applications）というプログラミング言語があります。以下のようなプログラムを書けばできます。

Excelとpythonの両方でシミュレーションをするのはなぜですか。それぞれに利点欠点があるのでしょうか。

えっ！実習の目的確認しないで実習してませんか？実際にやって利点欠点を考えるのが目的なんですけど。目的を意識せずに実習しても、学びの取れ高が少なくなってもったいないですよ。

試行回数が多いほど信憑性の高いシミュレーションであると思います。どのくらいの試行回数の多さからが適切なのでしょうか。やはり、モデルによって異なるのでしょうか

それは数学で学ぶ領域なんです。標本調査と言って、元の集団の特徴を捉えるためにどれぐらいのサンプルが必要かを求める手法があります。

私のプレイしているゲームで『時間帯によって☆4(レアキャラ)の排出確率が変化する説』というのがあるのですが、この説の検証は授業の学園祭で飲み物を販売するシュミレーションの応用でできますか？（授業ででてきた表の、「販売個数」の項目を時間にして、その時間ごとに100回ずつガチャ引いて、度数求めて、…で考え方は正しいですか？）

さぁ、それはわかりません。正しいかどうかは、状況を正しく表しているかどうか、つまりモデルとして適切かということです。確率が変動しているかどうかを検証する方法は、数学で学んだ仮説検定の考え方でやるのが適切です。

Excelでサイコロのグラフを表示させるときに、10回や50回でやるとときどきメモリが0.5刻みになったのは、数が小さすぎるからですか。100回では何度やっても整数でした。

Excelは範囲指定してグラフの種類を選ぶと自動的にグラフを作成してくれるので便利ですが、適切な設定にならない部分があります。気づいたら自分で直します。10回であれば最大値は3程度です。Excelにしてみれば、整数だけかどうかはわからないので縦軸は0.5刻みになるでしょう。私が50回で試したところ、最大値は11程度で、縦軸は整数値にしかなりませんでしたよ。

販売個数が10個に対して、度数が8とはどういう意味ですか。累積確率がそのまま乱数になっているのはなぜですか。乱数を用いているのに、飲み物がおおよそ200個前後になり、傾向として表れるのはなぜですか。

問題文を丁寧に読みましたか？説明のスライドだけ見ていませんか？説明、聞いていましたか？なぜだか考えましたか？「度数」ですが、過去の販売実績から、1時間で10個売れた回数が8回あったということです。「累積確率」ですが、考え方が逆です。累積確率によって0から1までの範囲を分割しておいて、乱数によってどの範囲が該当するかを調べ、その販売個数をその時間の販売個数と考えるということです。「傾向」についてですが、傾向があるから傾向として現れるのです。授業で説明した例だと、過去の販売実績から、起こりやすい販売個数が選ばれやすいように累積確率を用いて範囲分けをしました。乱数は偏りがないことが前提になっているので、均等に選ばれることが多く起こるので、100回もやれば傾向が見えてくるのです。
数学的に考えると1時間で売れる個数は以下の式で求められ、23個になります。期待値というやつです。8時間ですから184個ですね。

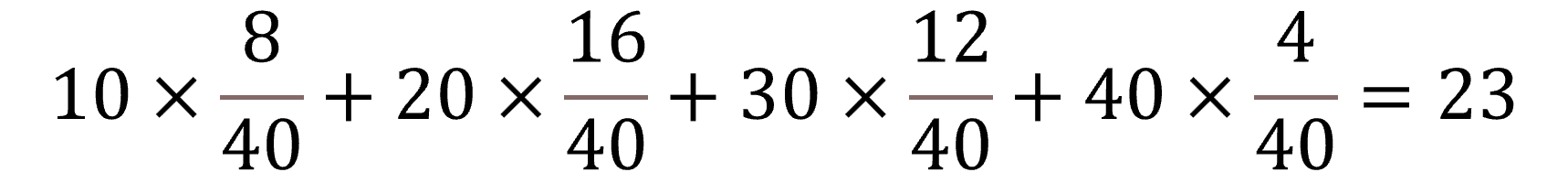
なぜこの方法で求めないかというと、元のデータ（販売個数のデータ）の集計方法が10個単位で、算術的に求めるのに向かないデータだからです。

先生はシミュレーションを授業以外で活用するときはありますか？

よく授業でお話ししていますが、ドライビングシミュレーターを毎日やっています（笑）。その他にも授業準備はシミュレーションの連続ですよ。スライドの手順で実際にできるか、間違える点はないかなど、皆さんがスムーズに授業を受けられるよう、事前にシミュレーションしています。

プログラミングには歴史がありますか？あるとしたらpythonは新入りですか？

現在使われているプログラム内蔵方式のコンピュータができた時点からプログラミングはおこなわれるようになっています。プログラムがなければ動かないんですから。授業でも説明したとおり、コンピュータにわかるようプログラムを書く必要があるので、最初は二進法や16進法でプログラムを書いていたわけです。コンピュータの性能が上がって、人間が読めるような定型文をコンピュータにわかるよう変換（途中に解釈は入らないので翻訳ではありません）できるようになり、プログラミング言語として使われるようになりました。最初のころはコンピュータに合わせてプログラミング言語があったのですが、最近では様々なコンピュータで同じプログラミング言語が使えるようになったという流れです。Pythonは比較的新しい言語で、1991年に登場し、1994年から使われるようになったそうです。

カウントをする時に0を代入する時としない時の違いが分からないです。

一般的に繰り返しなどの回数をカウントするときは初期値を0にして1ずつ加えることでカウントします。これは、変数を使ってカウントする方法です。変数を使ってカウントするときは、必ず初期値を設定しないとエラーになります。cnt=cnt+1という式を初期値なしに書くと、cntに初期値がなければ1を足すことができないからです。
0を代入しないときというのは、関数を使ってカウントするときのことを言っているのだと思います。saikoro.count(j+1)というやつですね。この関数はリストsaikoro内のj+1の要素の個数を数えることができます。個数を返す関数なので、いきなり「ポン」と個数として数値が出てきます。内部的な処理では初期値を0にしているかもしれませんね。

returnとはどういう意味なのか教えてほしい

returnですから、戻るという意味ですよね。自分で定義した関数の最後に書いてあるreturnのことだと思いますが、戻るということです。メインのプログラムから関数が呼び出され、関数でまとまった処理をしたら、元のプログラムに戻らなければなりませんよね。どこまでやったら戻るのか(つまり関数による処理の終わり)を宣言することになるのがreturnです。

感想より

ガチャのシミュレーションでは1万人でもそれほど当たることがなく、ガチャ課金の効率の悪さを実感した。こうして見ると、やりたいゲームなどの確率を計算させてから効率良く課金するということも出来るのではと思った。その代行サービスを提供するという選択肢もあるように思う。

数学で確率を学んでいて、高1の数学で計算できるのですから、自分でやってみればわかることだと思いますよ。代行サービスをやったら、「ぼったくり！」っていわれちゃいますよ。

一見、乱数を使えないように見えるものでも、範囲を決めてここからここまでの数字がここの範囲の度数になるようにすればつかえるのが驚いた。数学1の最後の単元のやつに似てると思った。

どのような内容だったんでしょうね。数学って世の中でとても役立っているのに、わかっていない人が多いんですよね。「社会に出たら数学なんか使わない」と豪語する人が時々いますが、その程度でしか仕事しかしていないということなんです。

ガチャの排出確率1%を1000回やって、Pythonでやると、10回中5回が90回台で、5回が100回台だったので、ほぼ1%だった

正しく乱数として機能しているということですよね。試してみることはとてもいいことです。

サイコロのシュミレーションで、１００回の時は出る目がばらつきサイコロとして使えそうだなと思って、１０００回にしたら１の目しかほとんど出なくなってしまい、とても驚いた。振る回数により、サイコロとして成り立たなくなってしまったのはなぜかとても不思議に思った。

それはあなたがExcelの式をコピーするのを忘れているからです。最初に100回疑似サイコロを振り、それぞれ何回出たか集計しました。疑似サイコロを1000振って、集計する式を1のところしか直さなかったからです。スライドには説明ありましたよ。

今日やったガチャのシュミレーションみたいに実際にああいった感じのプログラミングがゲームの中にされているのか知りたくなった。あの大量の情報をどこにしまい込んでいるのか、また少し省略したりして軽量化しているのか気になった。

ゲーム運営側がガチャで出た番号を覚えておく必要があるんですか？当たりはずれだけですよね、必要なの。100回分の当たり外れを覚えておく必要もなく、当たりの回数だけ覚えておけばいいので、一人当たり1バイトぐらい用意しておけば記録できますよね。

Excelやpythonを用いて、さいころ、ガチャのシミュレーションを行うことができた。randbetweenを使うことで、開始と終了の値を決めその中で乱数を発生させることができると分かった。さいころのシミュレーションを実際にやってみて、【F2】キーを押すことで乱数が変化し、値や分布が変化するのが面白かった。100回よりも1000回さいころを振った方が、データーの分布が一定になったが、完全に6つの目の出る割合が同じではないので、妥当ではないと思った。ガチャを100回行うシミュレーションを行うとあたりが1度も出ないときや5回も出る時があり、ランダムにあたりが出るようになっていたので妥当だと思った。コンピューターは繰り返しの処理が早く、正確であるためこのような何度も試行して、データを得る際にとても便利なものであると分かった。

完全に均一になることはないんですよ。計算しやすいように6回振ることにしましょう。均一に出るなら1回出るはずです。では、6回振ったとき、1が1回出る確率は求められますよね。7%ぐらいしかないんですよ。

関数の時は＝、変数の時は（）など、法則を見つけて意識しながらプログラミングをすることが大切なのだと知った。

法則じゃないんです。そういう文法で、決まり事です。決まり事をきちんと覚えないと、プログラムは書けません。

wordは簡単にグラフを作成することができいくつかの事象を比較するのにとても便利だと思った。pythonは自分がどんな命令をしているのか理解していないと意味がないと思った。最近複雑な命令が多くなり理解できないことがあるので、スライドをしっかり読んで、逐一自分が何をしているのか確認したい。

この授業、Wordは使ってないです。

ガチャの確率的シュミレーションをExcelで行った時、単純に排出回数だけが表示されてしまうので、何パーセントなのかといった具体的な確率が分からなかったです。分母で示すより、パーセントで確率が表示された方がパッと見て理解しやすいと思うので、その点を工夫してみたいなと思いました。

100人とか1000人でシミュレーションしたので、パーセント表示は必要ないと思ったのですが、計算式作れば良かったですかね。100人中65人に当たりが出たら65%なので、計算いりますか？

情報の授業でやるのは、共通テストで必要になるので日ごろの学習を大切にしていきたいなと思いました。見ながらやるプログラミングはできるけれど、見ずにやるとたぶんできないので、本質を理解しながら学んでいきたいなと思いました。

共通テストではプログラムを書くことはできませんよね。アルゴリズムを理解したり、動作を追えることが大切です。そのためにはプログラムを書く経験をして、うまくいかない経験をたくさんすると良いはずなんです。言語もDNCLという日本語表記で、命令を覚える必要もありません。

たまに漫画などで「～の確率～％」みたいなことを言っていることがあるが、あんな具体的な数字を頭の中で乱数でたくさんシュミレーションして求めることは出来ないと思う。ではあれは一体どのような計算で出している確率なのか気になった。もしかしたら数学で習うような確率なのかもしれない。

情報では確率をシミュレーションで求めたりしますが、確率は数学の理論に基づき計算できるものです。たとえば、1%の当選確率の100連ガチャって、当たる人が60人ぐらいだったと思います。数学の確率の手法で計算すると以下のように6割ちょっとだということが求められます。

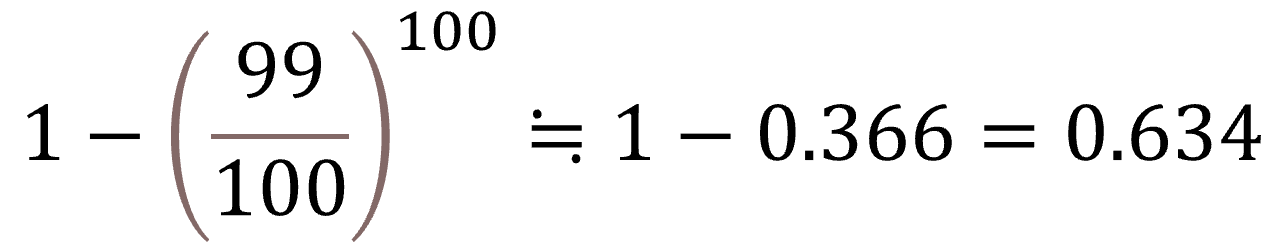
ま、暗算でできるかどうかは別ですけどね。

コンピューターを利用したシミュレーションは計算は正確だけど、仕入れの量や売れ行きの予想などはどんな条件が影響してくるか読めないし、経験や勘のほうが強いこともあるのではと思った。コンピューターを使うにしても、正しくシミュレーション結果を読み取って活用する力が必要とされると感じた。

経験や勘の方が有効であるならば、それはモデルが悪いということができます。とはいえ、シミュレーション結果は人間の判断の参考であるので、経験や勘を組み合わせて活用すればよいのです。

パイソンでプログラミングエラーが出たとき、スペルミスはもちろんだがエラーが出ている前の場所で抜けている箇所がないかを確認するのも大切だと思った

最初の数値見ただけでは確率がどこに使えるのかと考えていたが、累積確率から全体のうちでどれだけ当たりやすいかを考えられるのはとても便利だと思った。

膨大な数はコンピュータに計算させて人がその結果をもとに判断するのが一番合理的なのかなと思いました。

「import matplotlib.pyplot as plt」のような、初見ではかなり理解しにくく見えるプログラムでも、「as」は意味が理解できる単語であったため、そこからこのプログラムの意味をある程度理解できた。このように前から知っている単語などの知識を元に、見慣れないプログラムでも、その意味をある程度理解できるように慣れていきたい。

さいころのシミュレーションの際、回数を１００回から１０００回に増やすだけですべての目の出る回数がほとんど等しくなって、回数が多いほど正確になるということを実感できた。回数をどれだけ増やしても文句を言わずに間違えて記録することもなくやってくれるのがコンピューターのメリットだなと思った。

サイコロのシミュレーションを行ったときに、サイコロを振る回数が多いほど、出目の出方が均等になるということに気づきました。グラフを表示したことによってそのことが分かりやすくなっていました。

サクシードをやってるだけでは学べない数学の実用的な方法を学べた。また、データを扱う際には数学の知識が必須なので情報と数学は切っても切れない関係なのだなと再認識した。

飲食店（食べ放題とかも）は廃棄ロス削減のためどうやって売り上げ予想をしているのか疑問でしたが少し疑問が解けた気がします。あとガチャに沼るのはやめようと思いました。でもたまに当たりまくることがあるのでやめられません。ゲームのガチャは本当にランダムなんですかね。。。

確率的シミュレーションは数1の仮説検証という単元で出てきた確率問題と酷似していた。どのように統計を取るのかは特に情報で、それらの統計からどのように判断するかは特に数学で必要とされるものだ。科目によって一連の流れの中でどの部分を重要視するかが異なっていた。科目の間に繋がりがあることが改めて分かった。一つ一つの科目を丁寧に学んでいくことで、それが他のことや更に高度なことをやろうとした時に役に立っていくのかなと思った。

確率的シミュレーションを行う時にはプログラムかExcelを使うといいが、シミュレーションによって適正があるのでしっかりと見分けることが大切だと思う。Excelは表の形なので一回一回のデータを見るシミュレーションに適していて、プログラム言語はより多くのデータを結果だけ見たい時に適していると思う。なのでシミュレーションしたいものによって使うツールを使い分けたいです。

確率的モデルは、前回の確定的モデルのシミュレーションとは違い、条件によって確率が変動するため、何度もシミュレーションし直すと結果が多少変動し、繰り返しシミュレーションすることで精度を上げられることがわかった。表にしたとき、棒グラフだと条件の変化で見た目がかなり変わったが、箱ひげ図だとあまり変わらないように見えるのが面白いと思った。

割合を累計確率の差を使って、乱数を使った確率のプログラムを作れると分かった。これは様々ななシミュレーションに応用できると思った。

今回のシミュレーションで、一見確率とは関係のないようなものでも確率的な要素が含まれていることがあると言うことがわかった。また何度やっても全体として見るとほぼ同じ結果になるのは面白いなと思った。

今回は、確率を用いてシミュレーションをした。大学入学共通テストで、一見確率なんて使わないような問題でも、穴埋めの埋まっているところの数値を読み取り規則性を見つけ、シミュレーションをしていく。シミュレーションの授業を通して、コンピューターを活用する今後の世界で人間に求められる能力は、規則性を読み取る力だと考えた。今後の生活で効率化を図りたいときに、その作業の規則性を見つけ、アルゴリズムを組み立て、コンピューターに作業を任せ、早く正確なシミュレーションやプログラムを実行したい。

今日の授業では、曖昧になっていたプログラミングにおける関数と変数の違いや特徴について確かめることができたので良かった。サイコロのシミュレーションはどういうプログラムの理由があるか理解できた。

今日はシミュレーションの実習を行った。パイソンでプログラミングを書いていると、指示どうりの書き方以外にも、細かく変えられる部分があるなと思うことがあり、プログラムを書くのが楽しかった。

自分でプログラミングを書いてて最初はよくわからなかったけれどとりあえず書き終えて書いた内容をよく見て数値をいじってみたりしたらそれぞれの関数がどのような役割をしているかがよくわかった。

箱ひげ図や棒グラフに表すと分かりやすかった。目に見えるって大切だなと思った。選択する範囲が広かったのでどうするのがいいか調べたらshiftキーが便利だった。

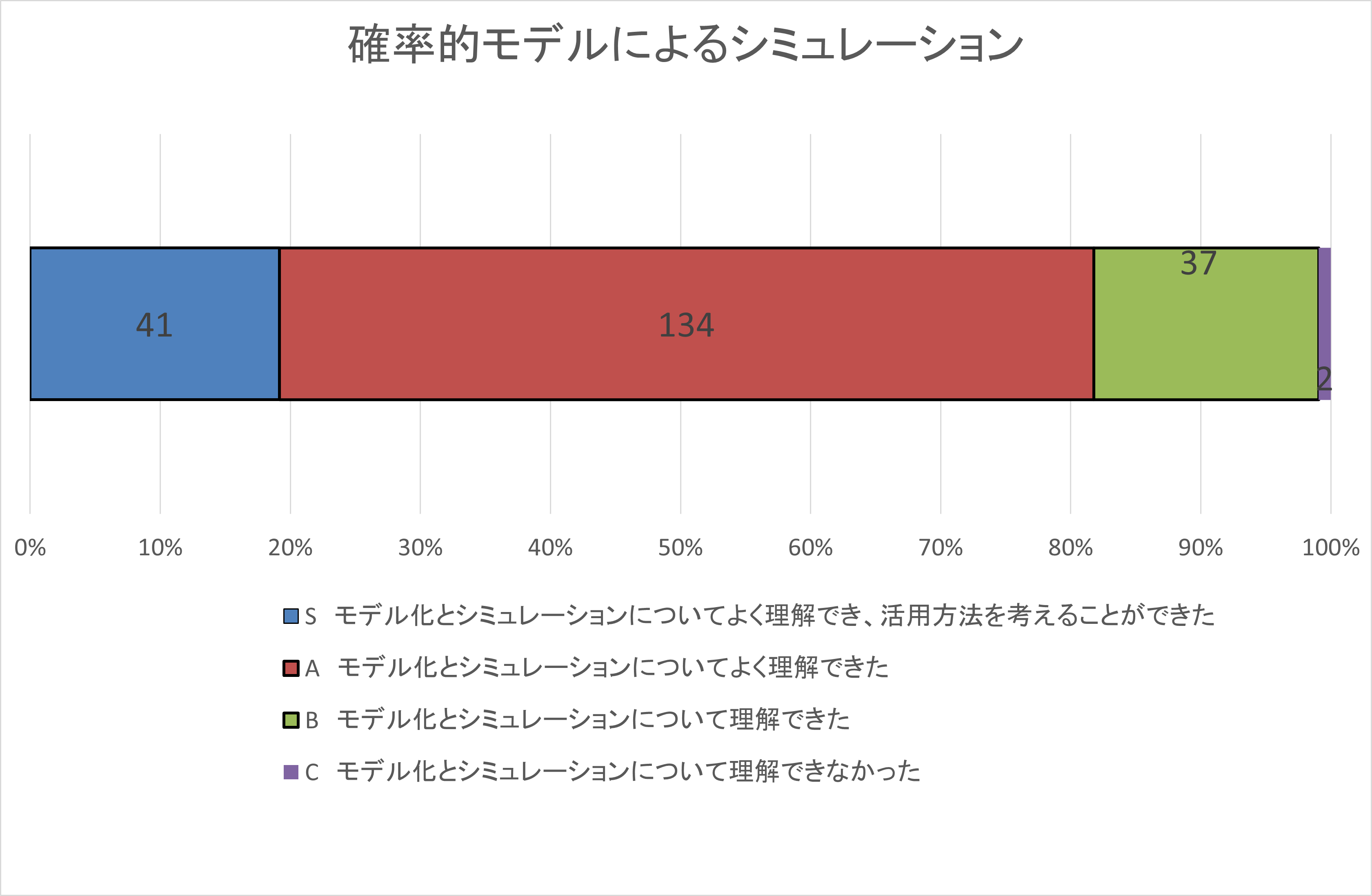
自己評価集計

ワードクラウド

３つのキーワード

---

感想や気づき

---