質問より
- 「1111」と書いてあったとき、15と-1はどのようにして見分けるのですか。
- 授業できちんと説明しています。最初に「正の数のみ」か「正負の数」か宣言することになっています。本来は単独で1111と書いてあっても判断できませんが、宣言がない場合は「正の数のみ」と考えます。
- 何故、小数の計算で起こるのは誤差であってエラーではないのか。
- エラーではありません。誤差です。コンピュータとはそういう仕組みなので、「仕様」です。あらかじめ許された誤差です。
- コンピュータのプログラムは規模が様々だと思うのですが、どのプログラムもAND・OR・NOTの3つの回路だけで動かせるものなのでしょうか。
- プログラムにはAND・OR・NOTは使われていません。論理回路は計算の仕組みです。コンピュータはどこで計算しているんでしたっけ?演算装置であり、CPUですよね。
CPUは授業で学んだ基本論理回路だけで作られることは無く、さまざまな処理ができるように別の回路も用意されています。ここで学ぶべきことは、電子回路で計算できる仕組みです。コンピュータのCPUについて理解するためには、もっと深く専門的に学ぶ必要があります。 - DSにはDSのOSを入れる必要があると仰っていましたが、例えば極端な話、DSにWindowsの OSに入れたらDSで Windowsが使える、ということはできるのですか?
- OSを利用するためには、ハードウェアがOSに対応している必要があります。DSのハードウェアはWindowsを動かすには能力が足りず、Windowsにも対応していません。古いWindowsパソコンにChromeOSを入れて使うことや、Windowsが利用できるPCにLinuxというOSを入れて使うことができます。どちらのOSもWindowsに対応したハードウェアに対応しているから利用できるのです。
- スライド内のPythonで計算してみようをやってみたのですが普通の計算の答えが出てきました。それであってますか?
- 普通の答えのものもあれば、普通じゃない答えのものもあります。環境や設定によっても違いがあります。
- コンピュータに限界があるのではなく、表示することに限界があると捉えてよいですか?
- 逆です。仕組みの話もしましたよね。計算上限界があるのです。表示上正しいように振る舞っているということです。
- いまいちコンピュータというものが理解できないのですが、コンピュータが動くときに、演算する(2倍する、負の数を表す、繰り上がりを無視する)とはどういうことですか?/半加算器の使い方と全加算器の使い方がいまいちよくわかりません。教えてください!!/加算器はなんのためにあるのですか。
- すべて順を追って授業で説明してきているんですけどね。コンピュータって超高速2進法計算機であって、それ以上のものではありません。なにか別の知能のようなものでも入っていると思っていませんか?コンピュータ上でできることは、すべて2進法の「演算」としてプログラムで表現されているのです。数値や文字・絵や音、動画などをどうやって2進法で表すのか学んできたのは、2進法しか計算できないコンピュータで扱うために必要だからです。
マウスを右に動かすということは、マウスの位置を示すx座標を増やします。加算ですね。画像を赤っぽくするには、RGBのうちRの値を増やします。加算ですね。 - コンピュータは因数分解をどう解くんですか。
- 解の公式で解けますよね。
- pythonはどう勉強すればいいのですか?(永遠の課題?)
- 何度も言ってますが、基本的なプログラミングを一通り自分でやってみてください。
- OSは装置ですか。機能ですか。
- ソフトウェアです。装置ではありません。機能でもありません。
- ExcelやPythonなどで計算するときのビット数はどういった基準で決めているのか
- 計算に必要なビット数としてあらかじめ定めます。必要十分とされるビット数です。あまり増やすと計算の手間が増え、動作が遅くなります。
- 1が0.99999となることは理解できるが、0.99996などになる理由はなんでなのかが気になった(計算結果が同じ0.1にも関わらず、そのようになる理由もあわせて気になった。)
- 二進法を学んだときに、二進法では十進法の0.1を正確に表現できないことを学んだはずです。1学期の15回目ですね。二進法のどこまでの桁を計算するかによって、十進法の0.1を2進法で表した循環小数を、扱う桁数を変えて十進法に直すと以下のように変化します。0.0937500000000000→0.0976562500000000→0.0996093750000000
→0.0998535156250000→0.0999755859375000→0.0999908447265625
その上で、十進法の有効桁数の問題で、どこまで表示するかによって最後の桁が6や9になるのです。
そもそも、計算結果が0.1となる小数自体、正確に表現できていないので、誤差のあるもの同士で計算したら、新たな誤差が発生するはずですよね。 - なぜexcelの小数を含む計算で桁数を増やすと数がおかしくなり、他方おかしくならない数もあるのですかなぜほかの小数も0.1を組み合わせてできる数なのに正確に表示できるのですか
- 内部でどのような取扱いになっているかはわかりません。おそらくExcelとして十進法で0.1として扱うことになっている二進法の値と、二進法による計算結果が一致すれば0.1と表示されるのだと思います。
- 補数は反転して1をたすという話でしたが、それで得た補数で引き算を足し算にすればいいと言うことでしょうか。
- 普段使う数をコンピュータで扱うためには、引き算をするだけでなく、負の数を表すこともできないと困りますよね。そのための方法です。
- 論理回路はソフトやプログラムに入っているのではなく、コンピュータ自体に組み込まれているということですか?
- コンピュータの計算ってどこでやっているんでしたっけ?演算装置ですよね。演算装置って何に入っています?CPUですよね。コンピュータ自体といったいい加減な解釈でなく、正確に理解しておいてください。
- コンピュータが引き算をする時と、割り算をする時どのように加法に直して計算しているかよくわからないです。
- 負の数を表現できるようになると、引き算ができるようになることはわかりますよね。5-3=5+(-3)とすれば、加法として計算できます。負の数の考え方は授業で説明しました。手早く求めるなら「補数」を使ってください。
割り算は引き算に直せることは理解できましたよね。10÷3は10から3が何回引けるか求めればいいわけです。3回引けてあまりが1になります。 - 十進法から二進法、二進法から十進法の切り替えは毎回コンピューターの中でやってるのですか
- 内部では二進法で計算しています。結果も二進法で記録しているかも知れません。コンピュータとしては、画面表示も二進法にしたいでしょうね。二進法で表示されても人間には読み取れないので、十進法に直して表示してくれます。
- コンピュータの計算がおかしくなることがあるのはなぜですか
- 誤差の話とは別に、ということだと思います。計算がおかしくなるのは①プログラムに誤りがある(バグがある)②入力値が不適切である③操作が不適切である などがあげられます。
- 論理回路が覚えられません(多数)
- 覚える必要はありません。大切なことは「論理回路で計算できること」、「基本論理回路(AND・OR・NOT)の動作」、「半加算器、全加算器の動作結果(真理値表)」を理解することです。
- なぜ小数だと誤差が出るのか(多数)
- その説明を授業でしたのですが、理解できていない人が多いようですね。コンピュータは超高速2進法計算機です。十進法の0.1を二進法で表すと循環小数になることは、授業でも説明しました。そもそも、10進法の小数のほとんどが2進法で正確に表すことができないのです。普段使う分には問題ない程度に調整されていますが、表示桁数を増やすと誤差が確認できます。PythonとExcelで0.1が答えとなる計算をやってみました。細かいところまで見ると違いますが、小数第2位あたりで見れば0.1で実用上困りません。
- 二進法にすると誤差が出るのなら、十進法で計算できるコンピュータを作るべきだ(多数)
- どうぞ開発してください。これも授業で説明してあります。人間は種類を見分けるのが得意ですが、機械は種類を見分けるのが得意ではありません。二種類しかない二進法だから高速に計算できるのであって、十進法なら十種類の段階を判定する回路が必要になり、高速に処理ができなくなるのです。
感想より
- もし、二進数での計算で作業を最短化したとすると1~10倍の中だったら7倍が一番手間がかかると思った。手順としては①もとの数を2倍(結果をA)②もとの数を4倍(結果をB)③もとの数+A+B、と3手かかるからだ。
- いいですね。そうやって自分なりに考えてみること、そして手順を整理すること、こういったことがコンピュータを理解する上で大切です。では、20までならどうなるでしょう。考えると面白そうです。
- コンピュータは加法だけを使って四則計算をしていて面白いなと思いました。なぜ加法だけでしか計算ができないのかなと思いました。もし加法以外の計算方法もコンピュータに教え込んだら計算はもっと早くできるのかなと考えました。二進法で表すと計算を間違えてしまうということは、二進法で表さないで計算する方法をし組み込めばコンピュータも間違えないのかなと考えました。
- なんだかいろいろなことを考えていますが、学んだことをまったく活かせていませんね。加算器だけで四則演算ができるのに、他の回路を用意するとなると、回路をどれぐらい用意したらいいんですか?乗算器や除算器は加算器と同じだけ用意しますか?乗算をやっているとき、除算器は無駄になっちゃいますけど。加算器だけでできることが大切です。
二進法は0と1だけではっきりしているので、高速に演算できます。他の(例えば十進法)で計算するには、多段階を見分ける別の回路を用意し、計算することになります。中途半端な段階を高速に見分けることはできないので、どうやっても高速に計算できません。
二進法のメリットを活かして超高速計算ができるのですから、二進法の特性を理解して上手に使うことが求められているのです。 - コンピュータは小数を2進法で表すことが出来ないから誤差が生じるということは理解したが、なぜ0.99999が0.1と表すことが出来てるのか疑問に思った。
- コンピュータは何も理解していません。0.99999をどう表示するか、プログラミングされているということです。表示幅が狭ければ表示できる桁になるよう四捨五入するでしょうし、0.1との差がいくつ以下になったら0.1と表示するという処理もあると思います。すべて事前にプログラムの指示に従っているだけです。
- コンピューターはいつでも正確な値を出す装置だと勝手に思い込んで、全て正しいと思っていたけれど小数の計算になると誤差が出ることもあると知って驚いた。また、有効数字の範囲以内でできるだけ正確に表示してくれるため、普通に使う計算では困らないとはいっても、その多少の誤差がある値がそのまま計算されて積み重なれば、大きな誤差になってしまうし、金融絡みの計算で大規模な金額がコンピューターの計算で誤差が生じてしまうと、大損失を生み出してしまうかもしれないのでコンピューターに全てを任せ、絶対に正しいと信じるのではなく、人間による確認を怠らないことが大切だと分かった。
- コンピュータは足し算、引き算、掛け算、割り算すべてできるとおもっていたけど、できるのは足し算のみで足し算を掛け算に応用、引き算を割り算に応用していると知り、これもコンピューターの特徴である最低限の機能で働くと言うことなのだと考えた。
- 4.3-4.2が間違った結果になるのは、0.1が二進法に適用していないからだと授業中には理解しましたが、それがどのような影響を与えるかに興味を持ち、浮動小数点数にたどり着きました。多くのコンピュータで用いられる浮動小数点数は、桁数が多くても少なくても「10の〇乗」で表すため表せる数の範囲が広いというメリットがあります。しかし、0.1のような二進法で表せない数はある程度の桁数で値を切り上げたり、切り捨てたりし、値を「丸める」から、その後の処理で計算が狂ってしまうそうです。次にどうすれば丸め誤差を発生させる小数をコンピュータ上で表せるか考え、量子ビットというものなら「1でありかつ0」という1、0だけの普通のコンピュータの2進法とは違う進法を思いつきましたが、量子ビットは3進法ではなく、「1でありかつ0」を利用して多くの計算をとても早くできる、というだけのものであることが調べて分かりました。0.1のような2進法で表せない数は永遠に循環してしまうので、どうやっても丸めなければいけないものなのだと理解しました。
- あまり多くの数字を使いすぎると処理に時間がかかってしまうため、0と1の2文字で全て行うことにより、早く処理ができるのだとわかりました。
- コンピュータでの四則演算や二進法の負の数、二進法での十倍のやり方、半加算器を付け足し続けて、計算できる桁数を増やすだとか、今回の授業はいかにして手間を省くか、うまくやりくりして困難を容易にするかをまじまじと見ることができた授業だと思った。誤差なく2進数で表されている数同士の計算なら、(設定されてるビット数の範囲での)誤差のない数が出力されるはずだから、4.3-4.2で誤りが、出力されてしまうのはどちらかの数字または両方が、もとは無限小数でコンピュータでの計算は向かないから、誤差なく求めたいときは自分自身でやるか、計算を正確にやってくれるプログラミングかやるべきだと思った。
- コンピュータは完璧なように思っていたけれど、限界もあるのだとわかりました。限界はあるといっても2進法を使って一瞬で計算してしまうところはやはり人間と違うのだと実感しました。論理回路を見たことによってコンピュータの中でどのように計算が行われているのかがわかりました。
- 今回は、コンピュータの中の演算で実際にどのようなことが行われているのか学んだ。ビット数に応じて、数字を入力すると、一瞬にして、結果が出てくるが、それは本当は多くの加算機を通じて行われていることがわかり、その早さに驚いたとともに、コンピュータがどのような構造になっているかわからないが、計算結果が正しく出されない場面があることも知った。だから、うまくコンピュータの良い部分だけを利用できるような理解をする必要があると考えた。
- 実際に手や頭を動かしてみることで気付くことが多々あった。2進法の得意な計算は10進法と同じように考えて2倍、4倍、8倍・・・であることや、Excelでの小数の限界、負の数が出てくる計算の上手い仕組みなど、うわべに留まらないコンピュータの深い所まで掘り進んだ気がして楽しかった。
- 少しずつ加算器の仕組みがわかってきたような気がする。初めて、加算器というものを学んだときは仕組みが理解することができなかったが、先生の授業を受けて全部とはいかないもののだんだんと理解し始めてきた。確かに論理回路を利用して電気を流せばコンピュータは一瞬で計算できる。以前はコンピュータというものは非常に賢く魔法のような機械だと思っていたが、論理回路を利用して足し算を繰り返しているだけと考えれば案外たいしたことない。しかし、論理回路を学んでみればコンピュータを作り上げた人たちに対し尊敬の思いがわいてくる。
- 前からコンピューターはなぜあんなに早く1秒間に計算できるのか疑問に思っていたが、単純な計算を繰り返していると知って面白いなと感じた。またコンピューターは2進法で計算しているので計算の桁数は限界があるから、桁落ちを防いで計算の精度を上げるには計算の順序を工夫する必要があると感じた。そうゆうことも含めて計算には限界があるのだといえるのだと思う。
- 二進法で負の数を表す方法は以前の授業で知っていたがその仕組みは分かっていなかったので、パワーポイントの表を見て理解することができ計算方法を暗記する必要がなくなりました。
- 半加算器をみていたら、1と1のときのみ繰り上げたいからAND回路を通った結果がCになり、どちらかが1のときSを1にしたいからOR回路を使うけれど、繰り上がるときは0にしたいから、それとCの数をNOT回路にかけたものとをAND回路にいれてSとするのだと分かり、あの記号を見ているだけだとよく分からなかったけれど仕組み的には意外と単純なんだなと思いました。
自己評価集計
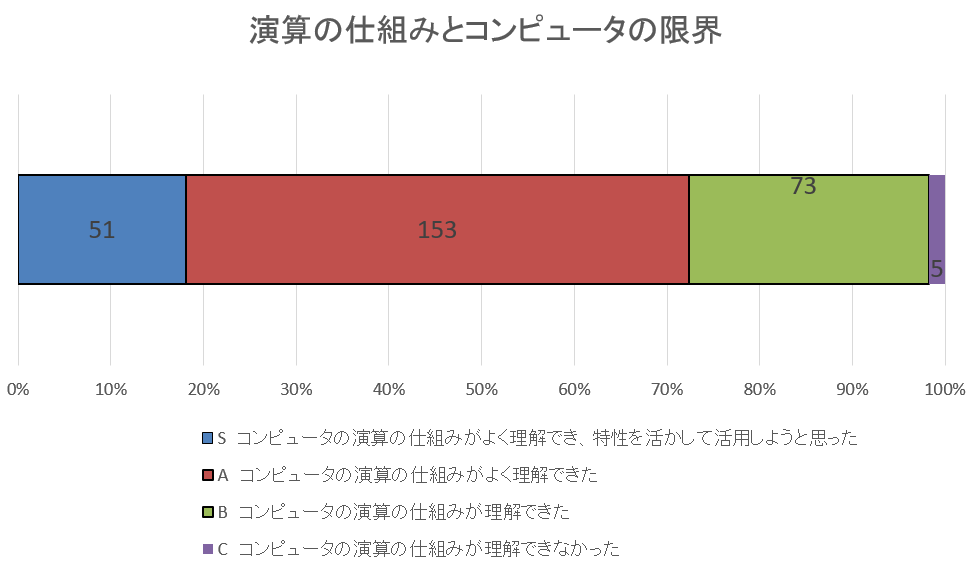
ワードクラウド
- 3つのキーワード
- 感想や気づき


前のページに戻る